Dalam machine learning, khususnya pada masalah regresi, evaluasi model sangat penting untuk menilai seberapa baik model dapat memprediksi output. Beberapa metrik evaluasi yang umum digunakan adalah Mean Absolute Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), dan Coefficient of Determination. Artikel ini akan membahas masing-masing metrik ini secara rinci.

Memahami Error Pada Machine Learning Regressi

Machine learning regressi bertugas untuk memprediksi data yang bersifat kontinu (bukan kategorikal). Untuk memahami sejauh mana performa model kita, metric yang biasa digunakan adalah error dan determinasi. Dalam statistik regresi, perbedaan antara data hasil prediksi dengn data yang sebenarnya disebut dengan residual. Nah, rata-rata residual secara agregat inilah yang disebut dengan error.

Untuk lebih memahaminya, coba perhatikan dulu gambar dibawah ini:

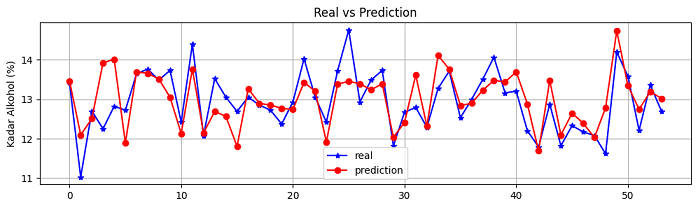
Gambar diatas adalah gambar perbandingan hasil prediksi kadar alkohol dengan data kadar alkohol yang sebenarnya. Prediksi dilakukan dengan menggunakan Linear Model. Kalian bisa mempelajari kelasnya disini.

Pada gambar diatas, garis merah dengan node lingkaran adalah data yang diprediksi (prediksi kadar alkohol). Sementara garis biru dengan node bintang adalah data yang sebenarnya (kadar alkohol yang sebenarnya). Nah, perbedaan satuan data yang diprediksi dengan data yang sebenarnya disebut dengan residual. Sementara yang disebut dengan error adalah rata-rata residual secara agregat.

Ada tiga teknik dalam machine learning regresi untuk memahami error secara agregat, teknik itu adalah: Mean Absolute Error (MAE), Mean Squared Error (MSE) dan Root Mean Squared Error (RMSE). Sementara untuk melihat seberapa baik (signifikan) hasil prediksinya, biasanya digunakan Koefisien Determinasi (R²).

Mean Absolute Error (MAE)

MAE adalah rata-rata dari nilai absolut perbedaan antara nilai yang diprediksi (y_pred) dan nilai aktual (y_true). Rumus dari MAE adalah seperti berikut:

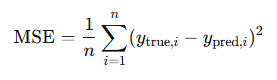
MAE mengukur seberapa besar kesalahan prediksi secara rata-rata. MAE mudah diinterpretasikan karena berbasis pada kesalahan absolut. MAE juga lebih tahan terhadap outlier dibandingkan MSE maupun RMSE.

Mean Squared Error (MSE)

MSE adalah rata-rata dari kuadrat perbedaan antara nilai yang diprediksi (y_pred) dan nilai aktual (y_true). Rumus dari MSE adalah seperti berikut:

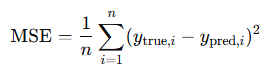
MSE cenderung memberikan penalti lebih besar untuk kesalahan besar (karena nilai kuadratnya), sehingga sensitif terhadap outlier. Biasanya, untuk mengembalikan nilai error kuadrat ke nilai yang sebenarnya dilakukan dengan menggunakan akar (root). Sehingga menghasilkan suatu besaran baru bernama Root Mean Squared Error (RMSE).

Root Mean Squared Error (RMSE)

RMSE adalah akar kuadrat dari MSE. Teknik ini digunakan untuk mengembalikan nilai error kuadrat ke nilaai yang sebenarnya. Rumus RMSE adalah seperti berikut:

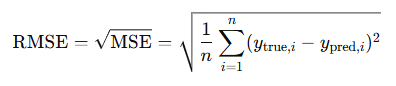
RMSE Memiliki unit yang sama dengan target variabel, sehingga lebih mudah diinterpretasikan dibandingkan MSE. Namun tetap sensitif terhadap outlier karena berbasis MSE.

Koefisien Determinasi (R²)

Koefisien determinasi mengukur seberapa baik model regresi menjelaskan variansi diantara residual. Nilai Koefisien Determinasi adalah antara 0 hingga 1. Nilai '0' berarti kesalahan prediksinya (variansinya) tinggi, sementara '1' berarti tidak ada kesalahan prediksi (prediksinya sempurna). Mirip cara perhitungan pada akurasi lah. Sementara jika nilainya dibawah '0' (negatif). Maka model dapat dikatakan tidak mampu melakukan prediksi.

Rumus dari Koefisien Determinasi adalah seperti berikut:

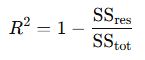
Dimana nilai SS_res adalah jumlah kuadrat residual secara agregat, dan SS_tot adalah jumlah kuadrat total secara agregat. Teknik ini paling sering digunakan dalam machine learning regresi karena memberikan pemahaman tentang seberapa baik model menjelaskan data.